—
データサイエンスの基礎として、
数学的な素養による数理モデルの構築と統計学的な素養による相関関係や因果関係などの関係性を見たり、確率分布による事象の予測モデルを構築したりできるようになる。
また、統計的検定を学ぶことでビジネスの意思決定が明確にデータで判断することができるようになる。
そこまで学んだ上で、昨今言われているAIと呼ばれる機械学習モデルに基づいたコンピュータサイエンスによるルール作りの話が注目されている。
ただし、私見では、数理演繹的な推論を適用するメタ理論を、現実のビジネスで発生する事象や現象の予測モデルに適用するための妥当性や蓋然性を誰が担保するのかという課題もあり、データを統計帰納的な推論によって、結果から原因を考えるという方法論が、今どんどん進化していっている。
ただし、
データサイエンスを偏重しすぎる弊害として、
数理モデルを考えるには、そもそも目の前に起きているビジネスの課題や事象などを主観的に自己がどのように捉えているかという問題の壁にぶつかる。
そして、統計的な因果や相関を見る場合でも、そもそもデータがないと帰納的な推論は一切できないという残念な課題感がある。
だからこそ、一般社団法人『データで考える力』イニシアティブにおいて、私が唱えている意味解釈法という研究法による理論、モデル構築の方法論をまずはデータリテラシーとして学ぶことが大事であると述べている。
質的研究法の中で、意味解釈法というメソッドは以下のようにマッピングもできる。
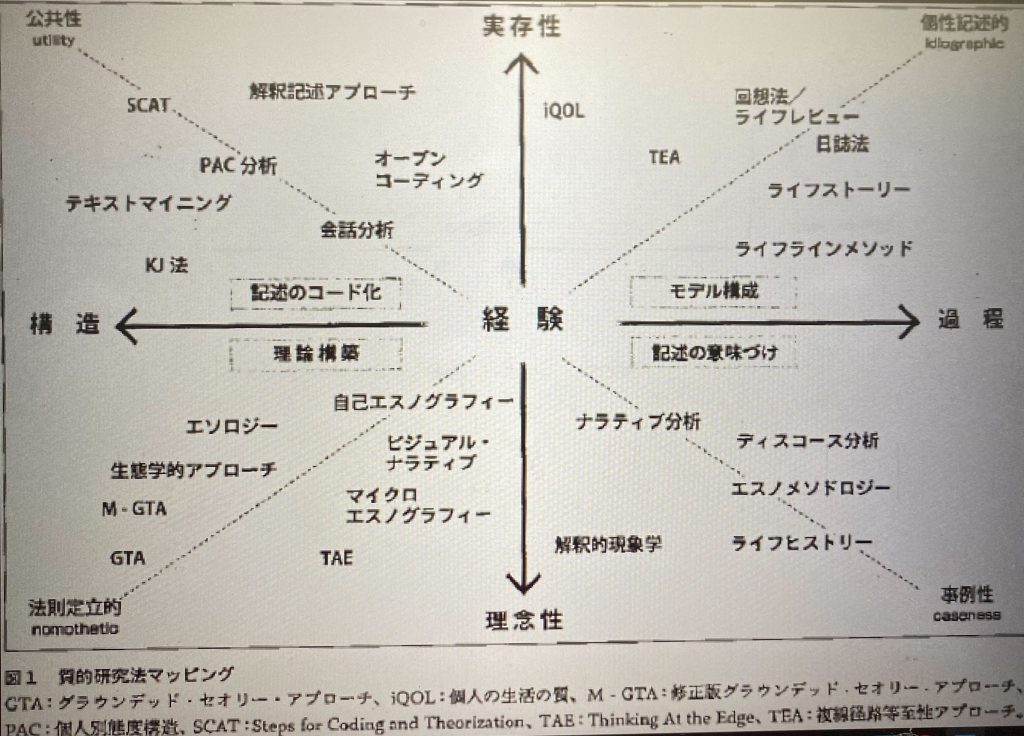
ここで大事なのは、抽象的な理論としての構造化を図るには、エスノグラフィックなアプローチも含めたグランデッドセオリーアプローチ(GTA)が適切であると考えているが、実際のビジネスの現場での実データ解釈には、オープンコーディングなどによる分類や実際の会話やコミュニケーション分析などの内容分析をメソドロジーに組み込んだ方法論を適用すべきとも考える。
どちらも構造を理論化したりしながら現実のビジネスへの対応を意味解釈していくには大事な方法論であることは明示的であると言える。
数学や統計学によって機械学習モデルを構築する前段の課題解決を方法論として学ぶべきと主張しているが、そうは言っても、メインディッシュである流行りのAIと呼ばれる機械学習モデルをどう作っていくかを改めて知っておくことも大事なので、そこは
これを踏まえて、掲題の通りにデータサイエンスを概観していってみることにする。
数理モデルの構築を含めて、数学としては、
- 確率・統計
- 微分積分
- 線形代数
- 集合・位相
という4つの分野がピックアップできる。
そして、機械学習モデルの構築については、以下のような手順を踏むが、
- 機械学習モデルを設計する ← 線形代数の素養を使う
- 誤差関数を定義する ←確率・統計の素養を使う
- モデルを学習する ←微分・積分の素養を使う
- モデルの動作を理解する ←集合・位相の素養を使う
という関係性によって、機械学習モデルを構築できるわけである。
ここまでの考え方で、今後のコラムにて数理モデル構築のための数学的な説明もしていこうと思う。
そもそも、ビジネスの現場でいかにデータからモデルを構築していくかという前段のプロセスが重要であり、モデル構築は専門家であるデータサイエンティストに任せるなりして、モデル構築前の工程をいかに実践するかが重要であり、教養としてのデータサイエンスを再度確認していきたい。
機械学習モデルの応用について
機械学習モデルの応用としては、複数のモデルを組み合わせることで高い精度を出力するアンサンブル学習というアプローチがある。
アンサンブル学習の種類は大きく分けて3つあり、
- バギング
- ブースティング
- スタッキング
というものがある。
バギングは、並列的にモデル構築を行い、総合的な学習結果が得られるという意味において、バリアンスを抑えることができる。ランダムフォレストなどは、このバギングと決定木を組み合わせた手法である。
また、並列な処理をおこなうバギングとは別にブースティングは直列的に学習処理を行うアプローチを取る。最初のモデルで上手く推定できなかった部分を、重み付けを行って次のモデルでは学習効果の高いモデルでアプローチしていく手法である。
そして、ディープラーニングの基礎となる理論として、パーセプトロンという考え方があるが、「信号」と「重み」の出力を調整していくことで、0もしくは1の2値による神経回路のような伝達の流れを表現するアルゴリズムである。
機械学習とは、その入力に対して、文字通り機械がそのパラメータを調整してくれるものであり、それがニューラルネットワーク、さらにはディープラーニングへとつながっていく。
ニューラルネットワークは、信号や重みの数が膨大になって来た場合に、出力されるデータと観測値との差分をいかに最小限度に抑えるかというのが課題となる。その場合、観測値と出力の二乗和誤差を求めて、それが最小になるパラメータを決めることが大事なってくる。つまり、微分を行って接線の傾きが0になるイコール最小値を取るという損失関数を決定していくことによってニューラルネットワークのアプローチが可能となる。
さらに、ニューラルネットワークの層構造を複雑にしたものがディープラーニングである。ディープラーニングでできることは、大きく2つ、
- 画像認識
- 自然言語処理
である。
画像認識は、畳み込みニューラルネットワークがベースとなり、大量の画像を読み込ませて学習させることで、畳み込み層を使った3次元のデータなどを情報を失わずにニューラルネットワークのモデルを構築していく手法によって、実現できる。
他に、機械学習は過去のデータから未来のデータを予測するモデルを作るものであるが、
数理最適化
というアプローチが存在していて、限られた制約条件の中でいかに最適な解を求めるかを考える方法論がある。
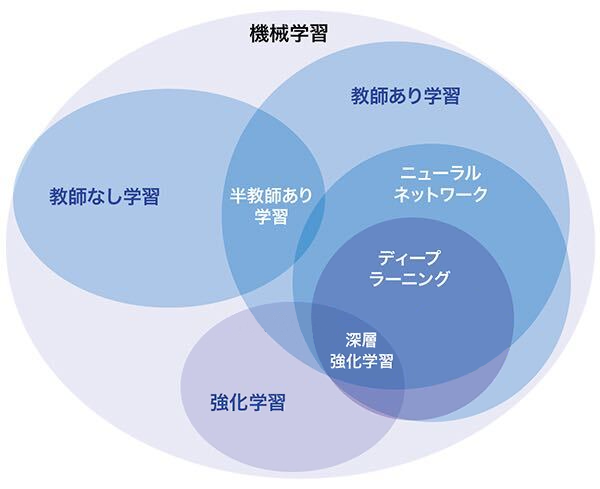
このように一言でAIがディープラーニングとイコールという関係性ではなく、AIというジャンルの中に機械学習が存在し、その機械学習の中にディープラーニングが存在している関係性であることも理解していた方が良い。
このように、ビジネスにおける事象や現象の予測モデルを機械学習でモデル化していく際に、まずは意味解釈法による変数の発見や関係性の仮説を持ちながら、データ・ドリブンに構造や特徴量を常にモデル化していく作業が必ず発生する。
そして、その前段がとても大事であって、むしろAIが進化していく過程においては、AI側のスキルが重視されているが、全くのゼロから変数を見定めていく際には、機械学習モデルよりも、ベイズ統計を用いた予測モデルを考えることをお勧めする。
ベイズ統計による事象の事前事後確率による予測モデル
ここまで機械学習モデルと数学の関係や数理モデルとの結合点について説明を行い、教養としてのデータサイエンスについて、簡単に説明してきたが、ビジネスにおける事象の予測モデルとしては、毎回、数理モデルを全て適合させる調整を課題ベースでやり遂げるには実務的に限界があると思っている。
条件付き確率分布による事象の予測モデルや因果関係を推測する考え方を結びつける方法論を、ベイズ統計モデリングとして、意味解釈法との組み合わせで、トライアンギュレーションとして成立させたいと考えている。
ベイズの公式は、条件付き確率の定義に基づいて表現され、以下のように数式で表すことができる。
P(c | r) = (P(r | c) * P(c)) / P(r)
ここで、P(c | r)は事後確率(cが与えられた条件下でrが起こる確率)、P(r | c)は尤度(cが与えられた条件下でrが観測される確率)、P(c)は事前確率(cの事前の確率)、P(r)は周辺尤度(rが観測される確率)を表す。
この公式は、事前確率と尤度を用いて事後確率を計算するための枠組みを提供するが、分母のP(r)を条件付き確率の総和で表現すると、以下のような数式となる。
P(c | r) = (P(r | c) * P(c)) / Σ[P(r | c’) * P(c’)]
ここで、Σはc’についての総和を表し、c’はcが成り立つ可能性のある全ての状態を示す。そして、P(r | c’)は各状態c’での尤度、P(c’)は各状態c’の事前確率を表す。
確率密度関数のケースで表現し、分母を∮(積分記号)で表現する場合は以下のようになる。
P(c | r) = (P(r | c) * P(c)) / ∫[P(r | c’) * P(c’) dc’]
ここで、∫は積分記号を表し、dc’は積分変数で、積分変数dc’は積分範囲と積分対象を示すが、離散変数以外の連続変数にも応用できることを示す。
つまり、事象r、cの前後関係を因果関係や予測モデルの推測に応用できることを示している。当然ここまでの話はすでに色々な場面で応用されているのは周知の通りであるが、データサイエンスだけを重んじだところで、大袈裟に言えば、この事象を把握するための理論構築ができないわけで、ここまでコラムで書くことで、第2回コラム以降で語ったデータリテラシーにも関係する意味解釈法との研究法のトライアンギュレーションをどう捉えるかという話に紐づいていくわけである。

